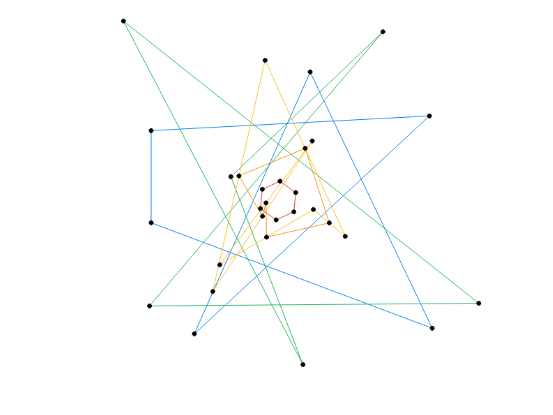
Petr’s Miracle, also called the “Petr-Douglas-Neumann theorem” is a geometric theorem that describes a procedure that can be applied to any arbitrary polygon to always produce a regular polygon with the same number of sides. In response to Mathologer‘s programming challenge at the end of their video on the topic, I created a web app to demonstrate the theorem.

Web App

The web app has a canvas to draw arbitrary polygons on and visualise the intermediate polygons towards becoming a regular one. The points (what’s the correct grammar here?) coordinates of every polygon is printed below. As explained in the video, there are toggles to apply angles in complementing pairs (can make the polygons prettier) and showing only every second stage of evolution (declutter the canvas). The “rescale & center” function works but unfortunately also transforms coordinates of any subsequent mouse clicks so I recommend finish drawing the starting polygon before rescaling & centering.